A Practical Guide to Scanning and Transmission Electron Microscopy Simulations

Colin Ophus; Stephanie M Ribet; Georgios Varnavides; Jacob Madsen; Toma Susi

Computational Article

Contents

Specimen Models¶

This chapter introduces the Atomic Simulation Environment (ASE) for creating specimen models for use in TEM image simulation.

ASE is a set of tools and Python modules for setting up, manipulating and visualizing atomic structures, which is used in conjunction with a large number of atomistic simulation codes, for example GPAW for running DFT simulations. In this notebook, ASE is introduced in the context of running electron microscopy image simulations with abTEM.

The `Atoms` Object¶

The Atoms object defines a collection of atoms. To define Atoms from scratch, we need to specify at least three things:

atomic positions,
atomic numbers (or chemical symbols),
a periodic cell.

For example, to create a basic model of the N₂ molecule, we could define:

atoms = ase.Atoms("N2", positions=[(0.0, 0.0, 0.0), (1.0, 0.0, 0.0)], cell=[6, 6, 6])

All these attributes of the Atoms object are stored in underlying NumPy arrays, which can be directly modified if desired. Convenient arithmetic operations such as + and * also directly work for the Atoms object, so structures can be easily extended and combined to create more complex specimens models.

Importing Structures from Files¶

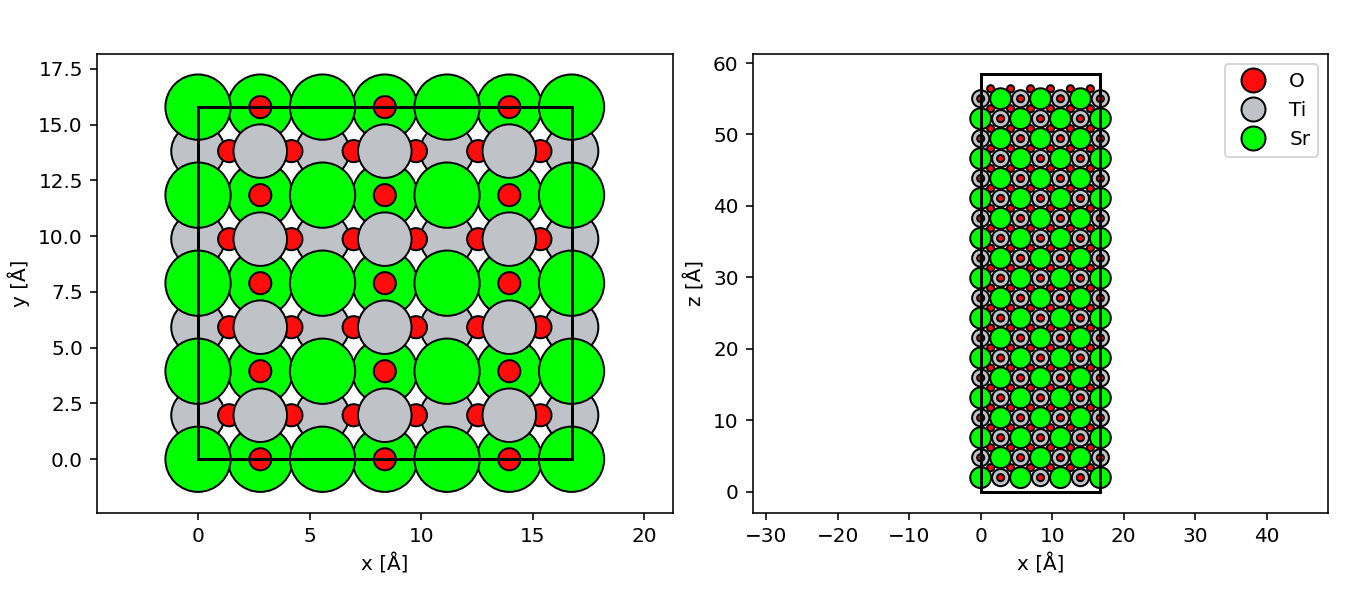
ASE can import all common atomic-structure formats (full list here). Below we import a .cif-file defining a unit cell of strontium titanate (SrTiO₃) that we provide with this text and will use in further examples.

srtio3 = ase.io.read("srtio3.cif")

Manipulating Atoms¶

abTEM always assumes that the imaging electrons propagate along the $z$ -axis in the direction from negative to positive coordinate values. Hence, to choose the zone axis, we need to manipulate the atoms so they are properly aligned.

ASE has many tools for manipulating structures, but one particularly useful one is the surface function, which can be used for creating a periodic surface (aligned with the $z$ -axis) for a given set of Miller indices.

In the widget below, we have oriented the strontium titanate structure along the (110)-direction and created supercells out of it, with 2 Å of vacuum added at the top and bottom surfaces.

Interactive widget showing supercell construction for the STO(110) supercell: — Figure 1.1:**Interactive widget showing supercell construction for the STO(110) supercell**:

Since the positions and atomic numbers are just NumPy arrays, they can be modified in-place. Below, we create an SrTiO₃/LaTiO₃ interface by changing the atomic numbers of the Sr atoms with a $y$ -coordinate less than $7.5 \ \mathrm{Å}$ in a (3,4,10) supercell oriented along the (110) zone axis. This interface created from a will be later used for STEM image simulations.

sto_lto = repeated_srtio3.copy()
mask = sto_lto.symbols == "Sr"
mask = mask * (sto_lto.positions[:, 1] < 7.5)
sto_lto.numbers[mask] = 57

Non-Orthogonal or Tilted Specimen¶

Most multislice implementations also require the supercell axes to be orthogonal, which can sometimes be non-trivial to achieve for a given crystal structure, but especially tricky for rotated crystals. In abTEM, there are some tools to help achieve this as described in its documentation. While small beam tilts can be accommodated within the multislice formalism, for arbitrary rotations of a crystal or large-angle beam tilts, the Bloch Wave method may instead be more appropriate (as implemented in py4DSTEM and recently also abTEM).

Sampling¶

In any numerical implementation, continuous physical quantities such as potentials or wavefunctions have to be described on numerical grids. In abTEM, these are represented on a rectangular grid of $N_x \times N_y$ grid points (gpts) or pixels.

Given an orthogonal cell with the sidelengths $L_x$ and $L_y$ , in the $x$ and $y$ -direction, the real-space sampling (or dimensions of the pixels) is $\Delta x = L_x / N_x$ in $x$ and $\Delta y=L_y / N_y$ . The real-space coordinates thus take on only discrete values of

x_i = i \Delta x \quad i = 0,1, \ldots , N_x - 1, \\ y_j = j \Delta y \quad j = 0,1, \ldots , N_y - 1. \\

(1.1)

The Fourier transform of this grid of values (for example, a simulated exit wave) will also have $N_x \times N_y$ grid points. However, in reciprocal space (for example, a simulated diffraction pattern), the sampling is instead determined by the supercell dimensions (real-space extent of the potential) given by the inverse relations $\Delta k_x = 1/L_x$ and $\Delta k_y = 1/L_y$ . The reciprocal space coordinates thus take on values

k_{x,i} = - k_{x,\mathrm{max}} + i \Delta k_x, \\ k_{x,j} = - k_{y,\mathrm{max}} + j \Delta k_y,

(1.2)

where the maximum spatial frequencies (reciprocal-space extent) are imposed by the real-space sampling

k_{x,\mathrm{max}} = \frac{1}{2\Delta_x} \quad \mathrm{and} \quad k_{y,\mathrm{max}} = \frac{1}{2\Delta_y} \quad .

(1.3)

Finally, we want to stress the perhaps non-intuitive fact that although some codes allow the sampling of diffraction patterns to be separately set, due to the reciprocal pixel-wise numerical correspondence between the real and reciprocal spaces, the only true way to improve reciprocal-space sampling, i.e. decrease $\Delta k$ , is to increase the size of the supercell in $x$ and $y$ .

In abTEM we choose to retain the direct correspondence between the real-space extent of the potential and the reciprocal-space sampling, and only use interpolation to decrease the number of pixels along one direction to reach uniform sampling. You can find some more information in the abTEM documentation.

Guide to STEM Simulations

Wave Aberrations