Note that VAEs will yield latent vectors and (optionally) translation vector and rotation as outputs, and can be configured to use class as input.

Source:VAE

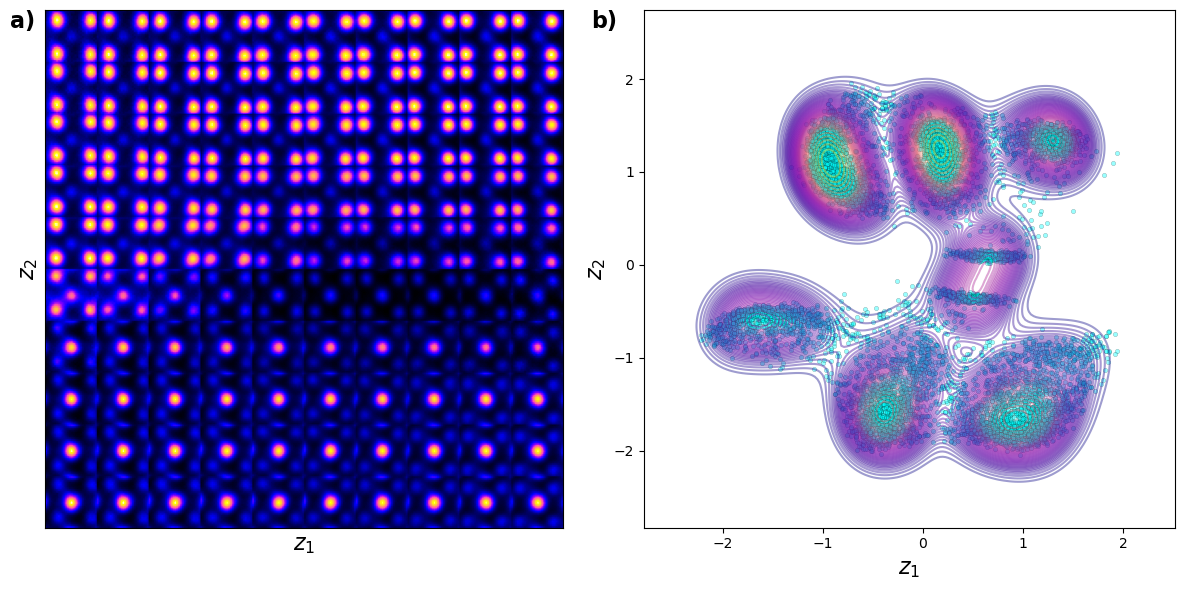
The latent representation of the system is visualized as a grid over the two latent variables $z_1$ and $z_2$. Each grid cell corresponds to a unique combination of values for $z_1$ and $z_2$ , which are decoded to produce corresponding reconstructions in the data space. The smooth and structured transition across the grid indicates that the model has learned a meaningful and continuous mapping between the latent variables and the data space. Variations in the grid reflect changes in the underlying physical structure, such as column type, domain orientation, or material properties.

The latent space distribution of the system reveals several distinct clusters. These clusters correspond to key factors of variation, including column type (primary variation factor), ferroelectric domain orientation, and the nature of the material (BFO vs. substrate). Notably, all these variations are effectively represented within just two latent variables $z_1$ and $z_2$.

Source:VAE

<IPython.core.display.HTML object>

interactive(children=(Dropdown(description='Variable 1', layout=Layout(width='250px'), options=('z1', 'z2', 'G…

<function __main__.plot_two_variables(variable1, variable2)>

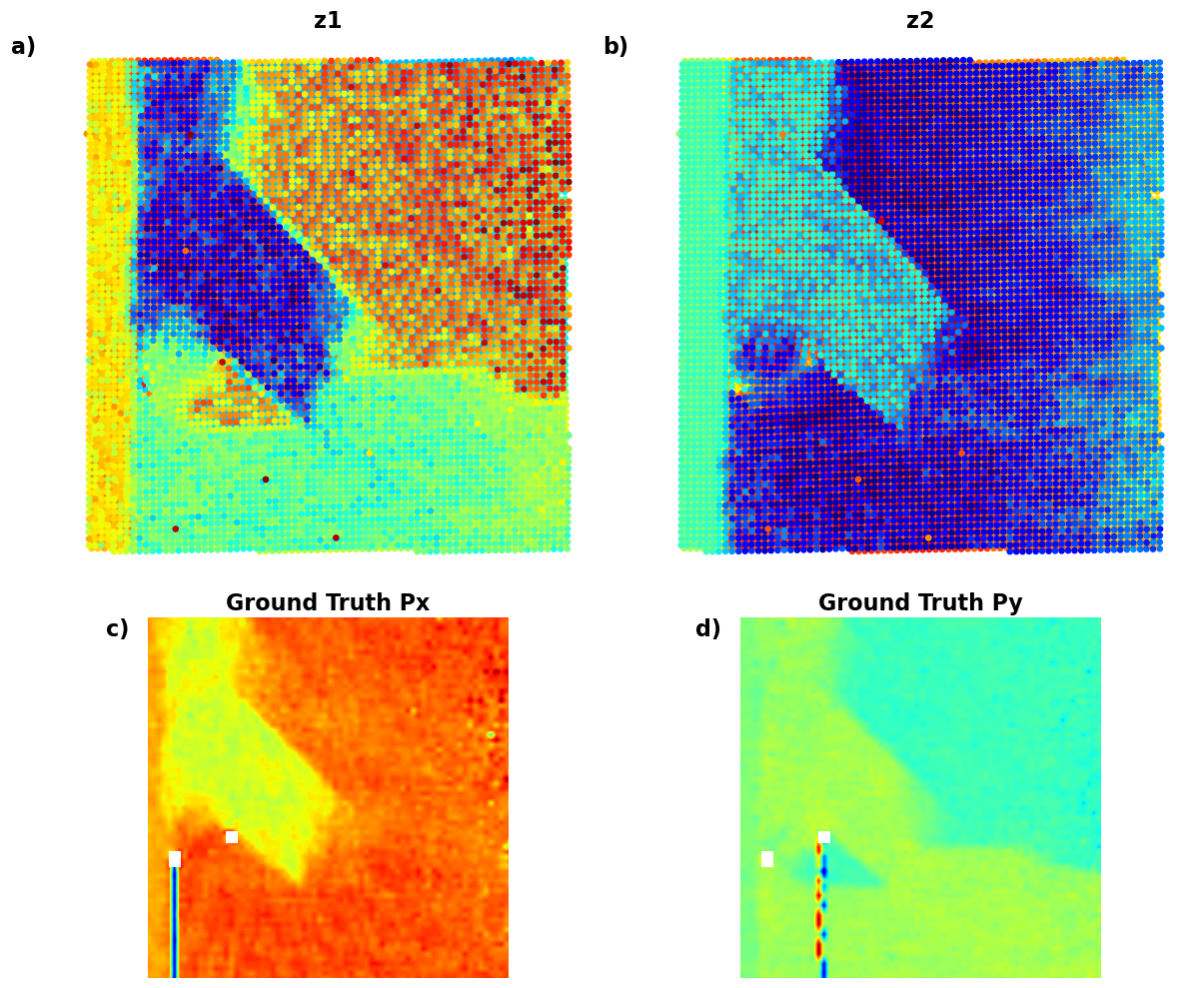
The VAE analysis highlights ferroelectric domains as regions with distinct contrast levels in the latent variables $z_1$ and $z_2$. The latent variable $z_1$ clearly differentiates between the substrate and the material, while $z_2$ exhibits a gradient effect on the right-hand side of the image, indicative of a mistilt effect. Additionally, the ground truth polarization components $P_x$ and $P_y$ are shown for reference.

However, this analysis reveals two primary challenges:

1. Lack of physical meaning in latent variables: While the latent variables effectively encode variations in the data, their physical interpretation remains undefined beyond their latent space representation.
2. Determining the optimal number of latent variables: It is unclear how many latent variables are necessary to comprehensively capture all meaningful variations in the system.

These limitations highlight the need for further work to ensure the physical interpretability of the latent variables and a systematic approach to selecting their optimal dimensionality.